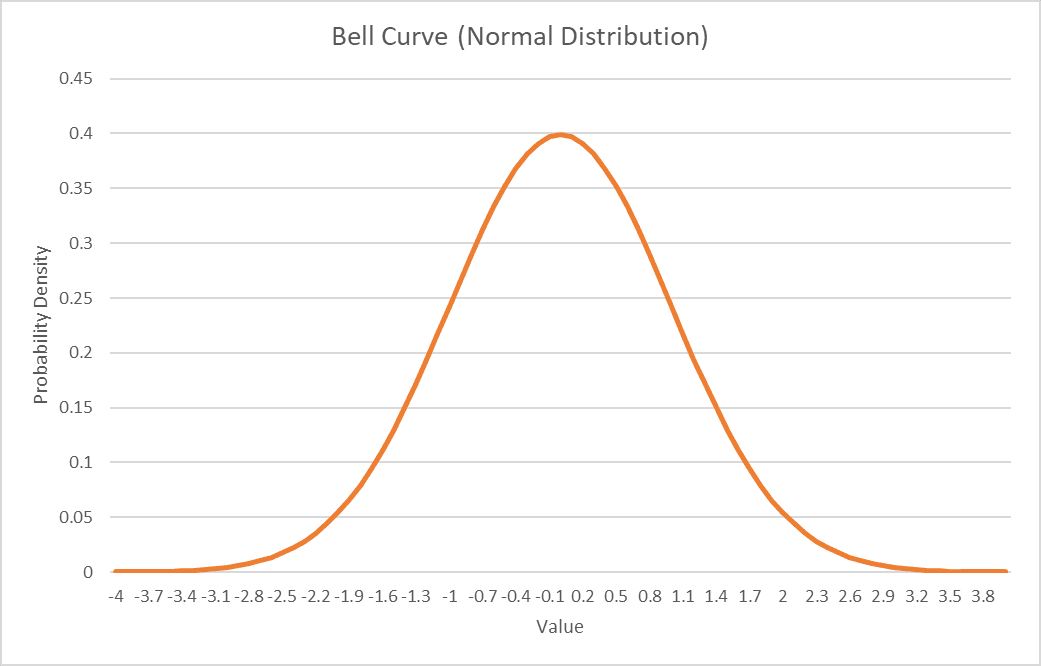
The Bell Curve Generator creates normal distribution curves (bell curves) using either manually specified parameters or from your actual data. You can visualize the normal distribution with custom mean and standard deviation values, or generate a curve that fits your dataset. This tool is perfect for illustrating probability distributions, comparing data to normal distributions, or creating statistical visualizations for presentations and educational materials.
If you need to calculate probabilities or z-scores for specific values, check out our Normal Distribution Calculator. For testing whether your data follows a normal distribution, use the Normality Test Calculator.
Calculator
Parameters
Related Calculators
Learn More
What is a Bell Curve?
A bell curve, also known as a normal distribution curve or Gaussian curve, is a symmetrical probability distribution that resembles a bell shape. It's one of the most important distributions in statistics, as many natural phenomena follow this pattern.
The curve is completely defined by two parameters: the mean (μ), which determines the center of the curve, and the standard deviation (σ), which determines the spread or width of the curve.
Key Properties of the Bell Curve
Shape Characteristics
- Perfectly symmetrical around the mean
- Mean, median, and mode are all equal
- Tails extend infinitely in both directions
- Total area under the curve equals 1
Empirical Rule (68-95-99.7)
- ~68% of data within 1 standard deviation
- ~95% of data within 2 standard deviations
- ~99.7% of data within 3 standard deviations
- Remaining 0.3% in the extreme tails
Creating Bell Curves in R
R provides multiple ways to create bell curves. Here are some examples:
Basic Bell Curve
# Create a bell curve with specific parameters
mean_val <- 100
sd_val <- 15
# Generate x values
x <- seq(mean_val - 4*sd_val, mean_val + 4*sd_val, length.out = 1000)
# Calculate normal distribution values
y <- dnorm(x, mean = mean_val, sd = sd_val)
# Plot the bell curve
plot(x, y, type = "l", lwd = 2, col = "blue",
main = "Bell Curve (Normal Distribution)",
xlab = "Value", ylab = "Density")
# Add vertical line at mean
abline(v = mean_val, col = "red", lty = 2)
# Add shaded areas for standard deviations
x1 <- seq(mean_val - sd_val, mean_val + sd_val, length.out = 100)
y1 <- dnorm(x1, mean = mean_val, sd = sd_val)
polygon(c(x1, rev(x1)), c(y1, rep(0, length(y1))),
col = rgb(0, 0, 1, 0.3), border = NA)Using ggplot2
library(ggplot2)
# Create data frame
df <- data.frame(x = seq(-4, 4, length.out = 1000))
df$y <- dnorm(df$x)
# Create bell curve with ggplot2
ggplot(df, aes(x = x, y = y)) +
geom_line(linewidth = 1.5, color = "darkblue") +
geom_area(data = subset(df, x >= -1 & x <= 1),
aes(x = x, y = y), fill = "blue", alpha = 0.3) +
geom_vline(xintercept = 0, linetype = "dashed", color = "red") +
scale_x_continuous(breaks = -3:3,
labels = paste0("μ", c("-3σ", "-2σ", "-σ", "", "+σ", "+2σ", "+3σ"))) +
labs(title = "Standard Normal Distribution",
x = "Standard Deviations from Mean",
y = "Probability Density") +
theme_minimal()Comparing Multiple Curves
# Compare bell curves with different parameters
library(ggplot2)
x <- seq(-10, 20, length.out = 1000)
# Create data for multiple normal distributions
df <- data.frame(
x = rep(x, 3),
y = c(dnorm(x, mean = 0, sd = 1),
dnorm(x, mean = 5, sd = 2),
dnorm(x, mean = 10, sd = 3)),
Distribution = rep(c("μ=0, σ=1", "μ=5, σ=2", "μ=10, σ=3"), each = 1000)
)
# Plot multiple bell curves
ggplot(df, aes(x = x, y = y, color = Distribution)) +
geom_line(linewidth = 1.2) +
labs(title = "Comparing Normal Distributions",
x = "Value", y = "Density") +
theme_minimal() +
scale_color_brewer(palette = "Set1")
Understanding Mean and Standard Deviation
Mean (μ)
The mean determines the center of the bell curve. It represents the average value of the distribution.
- Shifting the mean moves the entire curve left or right
- Does not affect the shape or spread of the curve
- The peak of the curve is always at the mean
Standard Deviation (σ)
The standard deviation controls the width and height of the bell curve. It measures the spread of the data.
- Larger σ creates a wider, flatter curve
- Smaller σ creates a narrower, taller curve
- Does not affect the location of the center